 |
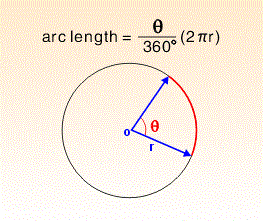
| arc length from radius and angle |
We've run across a similar question "answered" for eHow before, a topic addressed by Amy Dombrower (like Dombrower, Hodgson has a BA in journalism: see a pattern here?). What happened to Suzanne is pretty much what one might expect when someone with a BA attempts to answer a question about math beyond simple arithmetic.
Oh, Suzanne started out OK telling her readers that you need to know the radius to calculate this. It's at this point that she started getting herself in hot water: she rattled off several different ways to determine the radius. In the latest incarnation, Leaf says the methods are,
"r= d/2 r=c/2? r=?(A/?)" ......where "?" replaces the symbol π.That's not Suzanne's fault, by the way: her original list of formulas (at eHow.com, before the niching process) for the radius had the appropriate symbols and Greek letters. After that, however, Suzanne's solution went all wonky; presumably because she'd managed to confuse herself with all the letters and symbols. Here's one of her examples¹:
- Try Example 1. Let's say our circle has a circumference of 6 and an angle of π/2.First remember that r= c/2π.
- Plug 2 in for c so r=2/2π.
- r= .318
- Length would be s = θr
- Θ= π/2 r = .318s= π/2 x .318s=.49
- Our length of the arc is .49
| Suzanne got the right answer for her second example, but we suspect because it was just copied from an example somewhere else. At one point she said that you have to "find the radian [sic]" instead of the radius; a mistake that suggests she stopped taking math classes after middle school. Combine Hodgson's innumeracy with the blatant stupidity of whatever content editor let this rubbish pass, and you have a perfect Dumbass of the Day storm. ¹ We had to copy her example from an archived version at archive.org; the current version of the example at Sciencing reads something like "First remember that r= c/2?. Plug 2 in for c so r=2/2?. r= .318 Length would be s = ?r ?= ?/2..." Try plugging that into a calculator! |
copyright © 2018-2023 scmrak
MM - GEOMETRY
No comments:
Post a Comment