First Derivatives for Dummy Calculus Students

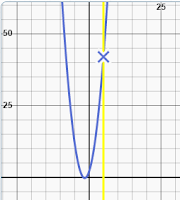
Graph of Kiran's function, x at 42,5

When the topic was mathematics, a lot of the eHow.com freelancers threw up their hands and thought something to the effect of. "Fuhgeddaboudit!" Others, apparently no better equipped to answer the question but braver (or more desperate for the stipend) decided to go for it anyway. When we found the post "How to Find the Slope of a Nonlinear Line" at Sciencing.com, we figured we'd found "case 2": Kiran Gaunle had found himself some useful references, but he managed to make a pretty serious error in "answering" the question.

Gaunle's two resources, both from online college math study sets, correctly pointed out the fact that the slope of a nonlinear function varies along the line; and that it is the slope of the tangent to the line at a given point. Further, at least one of them explained to him that the formula for the tangent is the (first) derivative of the function. So far, so good.

Kiran started off with the example equation f(x) = x²+3x+2, for which the first derivative is 2x+3. A little farther, still good. Next, he tried to calculate the slope of the line at X = 5. Gaunle first ran into trouble when he said he was going to,

"Identify a point where you want to calculate the slope. Suppose the slope is being determined at the point (5,5)."

Kiran's problem? That function doesn't pass through the point (5,5). If x = 5, y = 42. If y = 5, x is approximately 0.793.  Kiran gets the slope (13) correct, but it's a good bet that he doesn't understand what he just wrote (even a blind pig occasionally finds an acorn).

Alternatively, Gaunle suggested that his readers "draw" a tangent to the line at the point (2,3). Again, the line doesn't pass through that point: if x = 3, y = 20; if y = 2, x = 0. Although his example yields a slope of 1 for the point at which x = 3, in reality the slope is 9. This time the blind pig didn't find the acorn.

That's the kind of innumeracy we often see in our Dumbass of the Day candidates who, like Gaunle, have liberal arts degrees. Feh.

copyright © 2019-2021 scmrak

MM - CALCULUS